Solved

Compute the Inverse Laplace Transform of e−4tt4 e^{-4 t} t^{4}

Question 47

Multiple Choice

Compute the inverse Laplace transform of Compute the inverse Laplace transform of 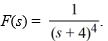. A) e^{-4 t} t^{4} B) e^{-4 t} t^{3} C) \frac{e^{-4 t} t^{3}}{3 !} D) \frac{e^{4 t} t^{4}}{4 !} E) \frac{e^{4 t}(t+4) ^{3}}{3 !} .


A) e−4tt4 e^{-4 t} t^{4}
B) e−4tt3 e^{-4 t} t^{3}
C) e−4tt33! \frac{e^{-4 t} t^{3}}{3 !}
D) e4tt44! \frac{e^{4 t} t^{4}}{4 !}
E) e4t(t+4) 33! \frac{e^{4 t}(t+4) ^{3}}{3 !}

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q42: Compute the Laplace transform of f:<br>F(t)

Q43: Find the Laplace transform of the

Q44: Consider the function<br><img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg" alt=" Consider

Q45: Compute the Laplace transform of f(t) =

Q46: Consider the function<br><img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg" alt=" Consider

Q48: Which of these statements is true?<br>A)

Q49: Compute the inverse Laplace transform of

Q50: Consider the function<br><img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg" alt=" Consider

Q51: Consider the following function:<br>F(t) = <img

Q52: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg" alt=" _. Here, δ