Consider the Second-Order Differential Equation $y(x)=a_{0}+a_{0}^{*}\left(x \ln x+\sum_{n=1}^{\infty} \frac{(-1)^{n} x^{n+1}}{n \cdot n !}\right)$

Multiple Choice

Consider the second-order differential equation .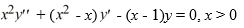
Using the method of Frobenius, which of these is the general solution of this differential equation? Assume 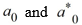are arbitrary real constants.

A) $y(x) =a_{0}+a_{0}^{*}\left(x \ln x+\sum_{n=1}^{\infty} \frac{(-1) ^{n} x^{n+1}}{n \cdot n !}\right)$
B) $y(x) =a_{0} x+a_{0}^{*}\left(x \ln x+\sum_{n=1}^{\infty} \frac{(-1) ^{n} x^{n+1}}{n \cdot n !}\right)$
C) $y(x) =a_{0}+a^{*}{ }_{0}^{x}\left[\ln x+\sum_{n=1}^{\infty} \frac{(-1) ^{n} x^{n+1}}{n \cdot n !}\right)$
D) $y(x) =a_{0}+a_{0}^{*} \ln x\left(1+\sum_{n=1}^{\infty} \frac{(-1) ^{n} x^{n+1}}{n \cdot n !}\right)$