Multiple Choice
Use the method of variation of parameters to solve the following third-order nonhomogeneous differential equation: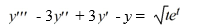
A)
B)
C)
D)
E)
F)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q1: What is the general solution of the
Q2: For which of the following homogeneous
Q3: Suppose a seventh-order homogeneous linear differential
Q5: For which of the following homogeneous
Q6: What is the form of a
Q7: What is the form of a
Q8: What is the least order of a
Q9: What is the form of a
Q10: For which of the following homogeneous
Q11: What is the form of a