Consider This Second-Order Nonhomogeneous Differential Equation:

Which of These $Y(t)=A t+B t^{4}$

Multiple Choice

Consider this second-order nonhomogeneous differential equation: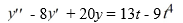

Which of these is a suitable form of a particular solution Y(t) of the nonhomogeneous differential equation if the method of undetermined coefficients is used? Here, all capital letters represent arbitrary real constants.

A) $Y(t) =A t+B t^{4}$
B) $Y(t) =\left(A t+B t^{4}\right) e^{4 t} \sin (2 t) +\left(C t+D t^{4}\right) e^{4 t} \cos (2 t)$
C) $Y(t) =A t^{4}+B t^{3}+C t^{2}+D t+E$
D) $Y(t) =\left(A t^{4}+B t^{3}+C t^{2}+D t+E\right) e^{4 t}(\sin (2 t) +\cos (2 t) )$
E) $Y(t) =\left(A t^{4}+B t\right) e^{2 t} \sin (4 t) +\left(C t^{4}+D t\right) e^{2 t} \cos (4 t)$
F) $Y(t) =\left(A t^{4}+B t^{3}+C t^{2}+D t+E\right) e^{2 t}(\sin (4 t) +\cos (4 t) )$