Consider This Second-Order Nonhomogeneous Differential Equation:

Which of the Following

Multiple Choice

Consider this second-order nonhomogeneous differential equation: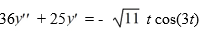

Which of the following is the form of the solution of the corresponding homogeneous differential equation? Here, C₁ and C₂ are arbitrary real constants.

A) $y(t) =e^{6 t}\left(C_{1} \sin (5 t) +C_{2} \cos (5 t) \right)$
B) $y(t) =C_{1} e^{-\frac{6}{5} t}+C_{2} e^{\frac{6}{5} t}$
C) $y(t) =C_{1} e^{-\frac{5}{6} t}+C_{2} e^{\frac{5}{6} t}$
D) $y(t) =C_{1} \sin \left(\frac{5}{6} t\right) +C_{2} \cos \left(\frac{5}{6} t\right)$
E) $y(t) =C_{1} \sin \left(\frac{6}{5} t\right) +C_{2} \cos \left(\frac{6}{5} t\right)$