Multiple Choice
Which of these is the general solution of the second-order nonhomogeneous differential equation 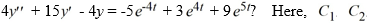 and all capital letters are arbitrary real constants.
and all capital letters are arbitrary real constants.
A)
B)
C)
D)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q105: Suppose a 160-lb object stretches a spring
Q106: Use variation of parameters to find
Q107: Which of the following functions Y(t)
Q108: Consider this second-order nonhomogeneous differential equation:<br><img
Q109: Consider this second-order nonhomogeneous differential equation:<br><img
Q111: Which of these is a fundamental
Q112: Which of these is the general
Q113: Which of the following is an
Q114: Which of these is the general
Q115: What is the solution of this