Which of the Following Is an Accurate Conclusion That Can

Multiple Choice

Which of the following is an accurate conclusion that can be made using the existence and uniqueness theorem for first-order differential equations for this initial value problem?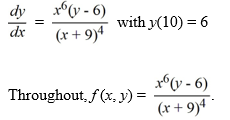

A) The initial value problem has a unique solution because f (x, y) is continuous on a rectangle containing the point (10, 6) .
B) The initial value problem is not guaranteed to have a unique solution because f_x (x, y) is not continuous when x = -9.
C) The initial value problem has a unique solution because both f (x, y) and f_y(x, y) are continuous on a rectangle containing the point (10, 6) .
D) The initial value problem does not have a solution because f_x (x, y) and f_y (x, y) are not both continuous on a rectangle containing the point (10, 6) .