Which of the Following Is an Accurate Conclusion That Can

Multiple Choice

Which of the following is an accurate conclusion that can be made using the existence and uniqueness theorem for first-order nonlinear equations for this initial value problem?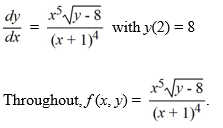

A) The initial value problem has a unique solution because f (x, y) is continuous on a rectangle containing the point (2, 8) on its boundary.
B) The initial value problem is not guaranteed to have a unique solution because f_x (x, y) is not continuous when x = -1.
C) The initial value problem has a unique solution because both f (x, y) and f_y (x, y) are continuous on a rectangle containing the point (2, 8) .
D) The initial value problem is not guaranteed to have a unique local solution because there is no rectangle surrounding the point (2, 8) on which both f (x, y) and f_y(x, y) are continuous.