Multiple Choice
Solve using the addition principle. Graph and write set-builder notation for the answer.
- 
A) 
B) 
C) 
D) 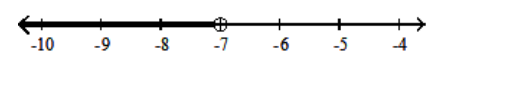
Correct Answer:

Verified
Correct Answer:
Verified
Q49: Determine whether the given number is
Q50: Solve.<br>- <span class="ql-formula" data-value="2(x+5)-(2 x+10)=0"><span class="katex"><span
Q51: Solve the problem.<br>-If the formula
Q52: Solve.<br>- <span class="ql-formula" data-value="5(2 z-3)=9(z+4)"><span class="katex"><span
Q53: Evaluate the formula for the given
Q55: Determine whether the given number is
Q56: Solve. Clear fractions first.<br>- <span class="ql-formula"
Q57: Solve.<br>- <span class="ql-formula" data-value="7 x+6=-15"><span class="katex"><span
Q58: Solve using the multiplication principle.<br>- <span
Q59: Determine whether the given number is