Solved

Solve the Problem x2+3xx^{2}+3 x B) x2+3x+1x^{2}+3 x+1 C) 4x24 x^{2} D) 4x4 \mathrm{x}

Question 249

Multiple Choice

Solve the problem.
-Find a polynomial for the sum of the areas of these rectangles.
Solve the problem. -Find a polynomial for the sum of the areas of these rectangles.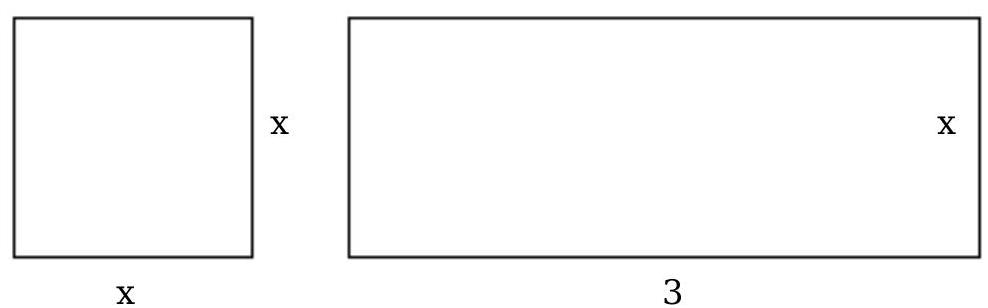 A) x^{2}+3 x B) x^{2}+3 x+1 C) 4 x^{2} D) 4 \mathrm{x}


A) x2+3xx^{2}+3 x
B) x2+3x+1x^{2}+3 x+1
C) 4x24 x^{2}
D) 4x4 \mathrm{x}

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q244: Perform the division.<br>- <span class="ql-formula" data-value="\frac{x^{4}+3

Q245: What is the meaning of the

Q246: Solve the problem.<br>-Find a polynomial for

Q247: Multiply.<br>- <span class="ql-formula" data-value="\left(x^{6}+6\right)\left(x^{6}-6\right)"><span class="katex"><span class="katex-mathml"><math

Q248: Divide and simplify.<br>- <span class="ql-formula" data-value="\frac{y^{-12}}{y^{2}}"><span

Q250: Write the word or phrase that

Q251: Multiply and simplify.<br>- <span class="ql-formula" data-value="3^{4}

Q252: Multiply.<br>- <span class="ql-formula" data-value="(3 x-4)(x-2)"><span class="katex"><span

Q253: Solve the problem.<br>-The distance <span

Q254: Multiply.<br>- <span class="ql-formula" data-value="\left(-5 m^{2}+m+7\right)(-5 m+2)"><span