Multiple Choice
Graph the absolute value function. State the domain and range
- 
A) Domain: ; Range: 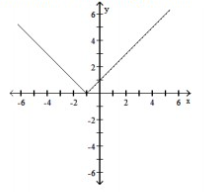
B) Domain: ; Range: 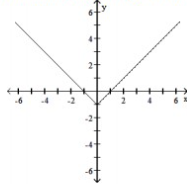
C) Domain: ; Range: 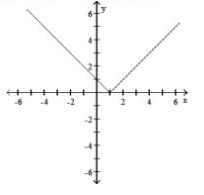
D) Domain: ; Range: 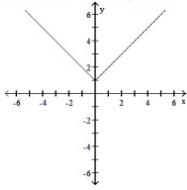
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q2: What is the difference between the
Q3: Rewrite the function as a piecewise
Q4: Write the word or phrase that best
Q5: Determine the missing inequality sign<br>- <span
Q6: Find the slope-intercept form of the
Q8: Determine whether the ordered pair is
Q9: Find the <span class="ql-formula" data-value="x"><span
Q10: Complete the table with ordered pairs
Q11: Find the slope-intercept form of the
Q12: Refer to the graph of the