Multiple Choice
Use the given graph of a rational function to solve the problem.
-Find r(3) .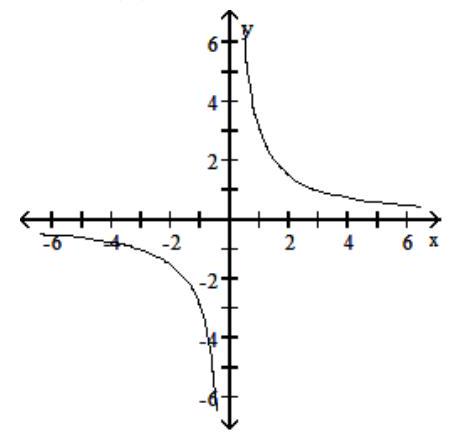
A) -1
B) -3
C) 0
D) 1
Correct Answer:

Verified
Correct Answer:
Verified
Q198: <span class="ql-formula" data-value="\frac{6}{(x+2)^{2}}+\frac{8}{x+2}"><span class="katex"><span class="katex-mathml"><math xmlns="http://www.w3.org/1998/Math/MathML"><semantics><mrow><mfrac><mn>6</mn><mrow><mo stretchy="false">(</mo><mi>x</mi><mo>+</mo><mn>2</mn><msup><mo
Q199: For the given rational functions
Q200: <span class="ql-formula" data-value="\frac{x}{x+4}-\frac{4}{x-4}=\frac{x^{2}+16}{x^{2}-16}"><span class="katex"><span class="katex-mathml"><math xmlns="http://www.w3.org/1998/Math/MathML"><semantics><mrow><mfrac><mi>x</mi><mrow><mi>x</mi><mo>+</mo><mn>4</mn></mrow></mfrac><mo>−</mo><mfrac><mn>4</mn><mrow><mi>x</mi><mo>−</mo><mn>4</mn></mrow></mfrac><mo>=</mo><mfrac><mrow><msup><mi>x</mi><mn>2</mn></msup><mo>+</mo><mn>16</mn></mrow><mrow><msup><mi>x</mi><mn>2</mn></msup><mo>−</mo><mn>16</mn></mrow></mfrac></mrow><annotation encoding="application/x-tex">\frac{x}{x+4}-\frac{4}{x-4}=\frac{x^{2}+16}{x^{2}-16}</annotation></semantics></math></span><span
Q201: <span class="ql-formula" data-value="\frac{x^{2}-10 x+21}{x^{2}+14 x+49} \div \frac{x^{2}-6
Q202: Find the domain of the rational
Q204: Simplify the rational expression. (Assume the
Q205: Identify the given function as a
Q206: Simplify the complex fraction.<br>- <span class="ql-formula"
Q207: <span class="ql-formula" data-value="\frac{4 x^{2}-7 x-5}{x^{2}+5 x}-\frac{3 x^{2}-2
Q208: <span class="ql-formula" data-value="\frac{x+5}{x^{2}+9 x+14}+\frac{5 x-4}{x^{2}+6 x-7}"><span class="katex"><span