Solved

For the Given Graph of a One-To-One Function F(x), Graph

Question 330

Multiple Choice

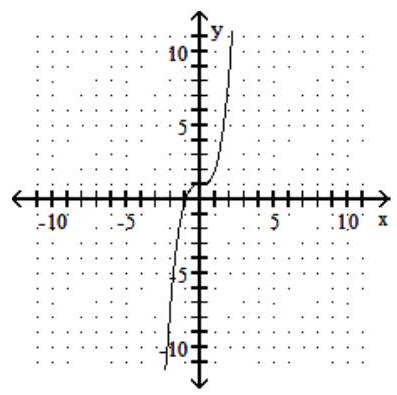
For the given graph of a one-to-one function f(x) , graph its inverse functionf-1(x) using a dashed line
-
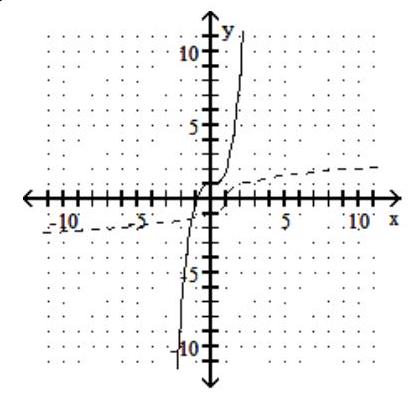
For the given graph of a one-to-one function f(x) , graph its inverse functionf-1(x) using a dashed line - A) B) C) D)


A)
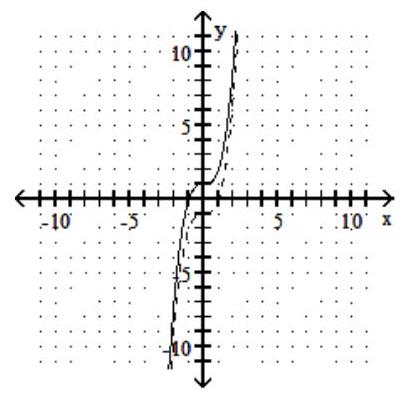For the given graph of a one-to-one function f(x) , graph its inverse functionf-1(x) using a dashed line - A) B) C) D)
B)
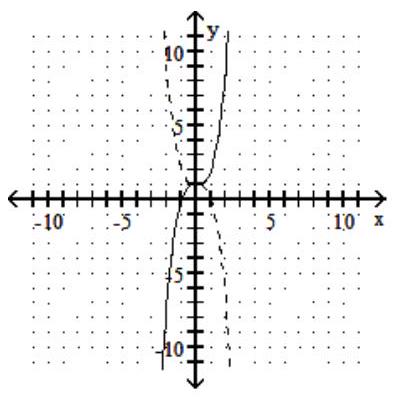For the given graph of a one-to-one function f(x) , graph its inverse functionf-1(x) using a dashed line - A) B) C) D) C)
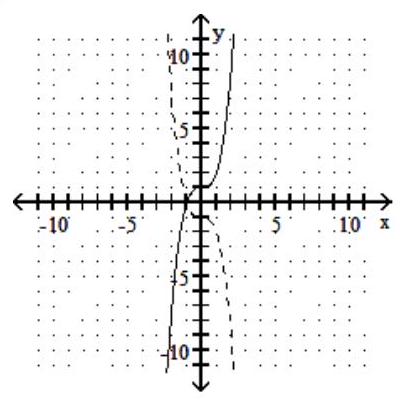
For the given graph of a one-to-one function f(x) , graph its inverse functionf-1(x) using a dashed line - A) B) C) D) D)
For the given graph of a one-to-one function f(x) , graph its inverse functionf-1(x) using a dashed line - A) B) C) D)

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q325: Evaluate the given function<br>- <span class="ql-formula"

Q326: Solve.<br>- <span class="ql-formula" data-value="\log _{4}(6 \mathrm{x}-7)=\log

Q327: Solve the problem.<br>-Find <span class="ql-formula"

Q328: Evaluate the given function. Round to

Q329: Given <span class="ql-formula" data-value="f(x)"><span class="katex"><span

Q331: Solve.<br>- <span class="ql-formula" data-value="2^{9-3 x}=1"><span class="katex"><span

Q332: Rewrite in logarithmic form<br>- <span class="ql-formula"

Q333: Determine whether the functions <span

Q334: Rewrite as a single logarithm using

Q335: Rewrite as a single logarithm using