Multiple Choice
For the given function , find and graph the function and its inverse.
- 
A) 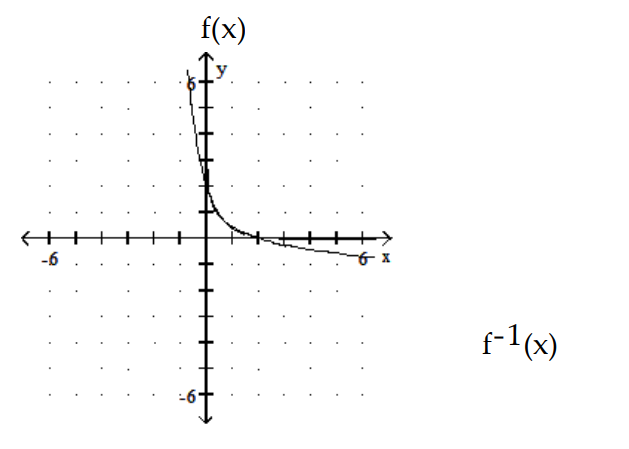
B) 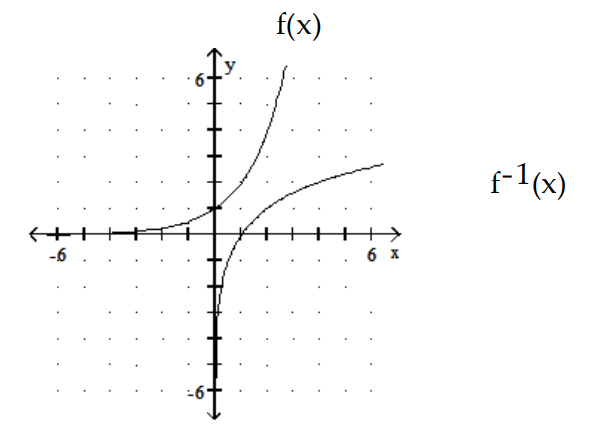
C) 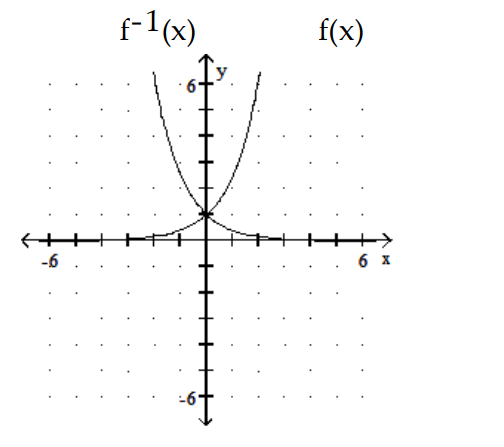
D) 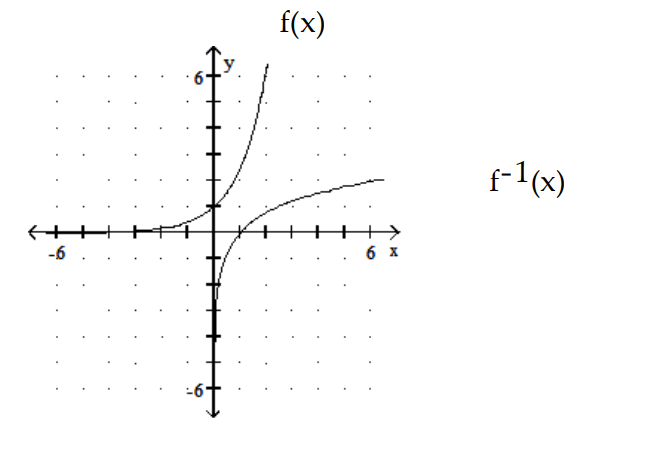
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q286: Rew rite as a single logarithm.
Q287: Evaluate the given function.<br>- <span class="ql-formula"
Q288: Rew rite as a single logarithm.
Q289: Solve the problem.<br>-The number of male
Q290: Graph. State the domain, range, and
Q292: The sales of a new product
Q293: Solve.<br>- <span class="ql-formula" data-value="2^{-4 x+12}=16"><span class="katex"><span
Q294: Determine the equation of the vertical
Q295: Rewrite in exponential form.<br>- <span class="ql-formula"
Q296: Solve the problem.<br>-Find <span class="ql-formula"