Multiple Choice
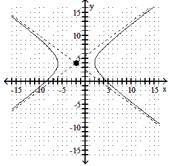
Find the standard-form equation of the hyperbola whose graph is shown.
-
A)
B)
C)
D)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q36: Graph the circle. State the center
Q37: Solve.<br>-A person at the top of
Q38: Graph the ellipse. Give the coordinates
Q39: Graph the hyperbola. Give the coordinates
Q40: Graph the parabola. State the vertex
Q42: Solve the system by the substitution
Q43: Graph the parabola. State the vertex
Q44: Solve.<br>-The planets in a certain solar
Q45: Solve the system by the substitution
Q46: Find the distance between the pair