Multiple Choice
Use the properties of parallel lines to solve the problem.
-In the figure, . Given this information, find the measures of as many other angles as possible.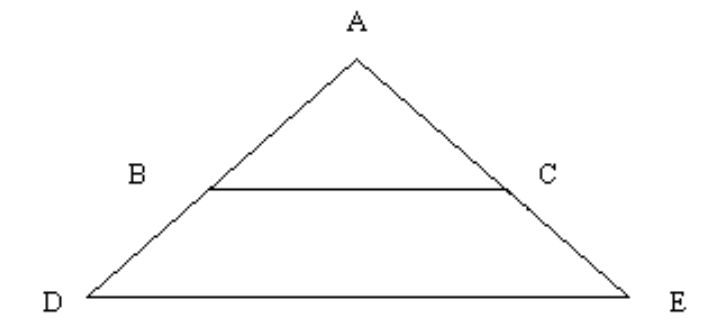
A)
B)
C)
D)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q154: Find the area of the shaded
Q155: Tell whether the angle is acute, right,
Q156: Classify the triangle as equilateral, isosceles, or
Q157: Solve the problem.<br>-Draw the segment whose endpoints
Q158: Find the measures of the indicated
Q160: Find the area of the shaded
Q161: Use a protractor to measure the
Q162: Determine whether the pair of triangles is
Q163: Find the volume.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9836/.jpg" alt=" Find
Q164: Solve the problem.<br>-How much will it