Multiple Choice
Use the properties of parallel lines to solve the problem.
-In the figure, . Given this information, find the measures of as many other angles as possible.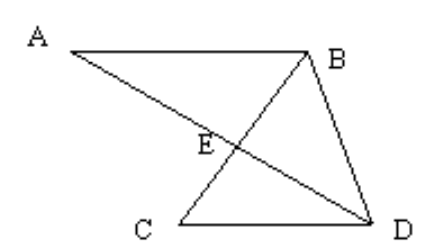
A)
B)
C)
D)
Correct Answer:

Verified
Correct Answer:
Verified
Q189: Classify the polygon by name.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9836/.jpg" alt="Classify
Q190: Find the circumference of the circle.
Q191: Find the sum of the angle
Q192: Find the area.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9836/.jpg" alt=" Find
Q193: Find the perimeter. Use 3.14 for
Q195: Find the perimeter of the polygon.<br>-<img
Q196: Find the volume of the circular
Q197: Classify the triangle as equilateral, isosceles, or
Q198: The triangles are congruent. Find the
Q199: Which property (if any), should be used