Multiple Choice
Solve using the addition principle. Graph and write set-builder notation for the answer.
- 
A) 
B) 
C) 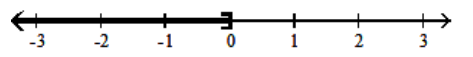
D) n n 
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q219: Solve the problem.<br>-If the formula
Q220: Solve. Clear decimals first.<br>- <span class="ql-formula"
Q221: Solve.<br>- <span class="ql-formula" data-value="6 x-(3 x-1)=2"><span
Q222: Decide if the given number is
Q223: Solve using the multiplication principle.<br>- <span
Q225: Determine whether the given number is
Q226: Solve the problem.<br>-By switching service providers,
Q227: Answer the question.<br>-In a school survey, students
Q228: Graph the inequality.<br>- <span class="ql-formula" data-value="x>-4"><span
Q229: Solve using the multiplication principle.<br>- <span