Multiple Choice
Solve using the addition principle. Graph and write set-builder notation for the answer.
- 
A) 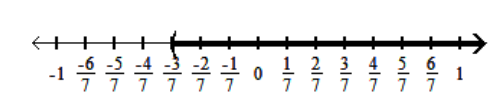
B) 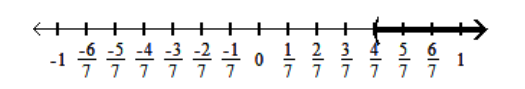
C) 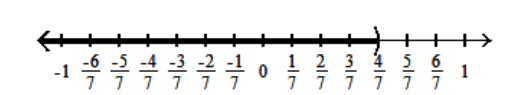
D) 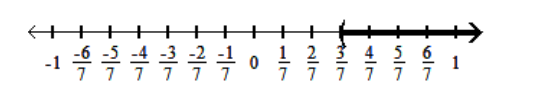
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q199: Determine whether the given number is
Q200: Solve. Clear fractions first.<br>- <span class="ql-formula"
Q201: Solve the problem.<br>-In order for a
Q202: Solve the problem.<br>-A rectangular Persian carpet has
Q203: Provide an appropriate response.<br>-The solution for
Q205: Solve the problem.<br>-The parking lot at
Q206: Translate the sentence to an inequality.<br>-Five
Q207: Solve.<br>- <span class="ql-formula" data-value="4 x-2+7 x-7=6
Q208: Solve the problem.<br>-If Gloria received a
Q209: Solve the equation using the addition