Multiple Choice
Solve using the addition principle. Graph and write set-builder notation for the answer.
- 
A) 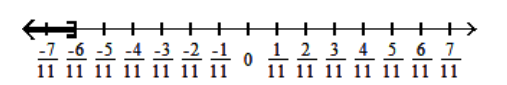
B) 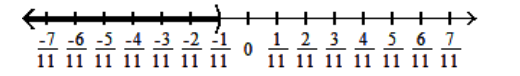
C) 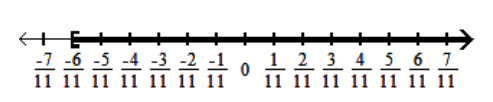 D)
D) 
Correct Answer:

Verified
Correct Answer:
Verified
Q23: Solve.<br>-The height of the tallest building
Q24: Solve.<br>- <span class="ql-formula" data-value="(y-11)-(y+8)=4 y"><span class="katex"><span
Q25: Solve using the multiplication principle.<br>- <span
Q26: Solve.<br>- <span class="ql-formula" data-value="2[3-(1-5 r)]-r=-2+3(2+3 r)"><span
Q27: Solve using the multiplication principle.<br>- <span
Q29: Solve.<br>- <span class="ql-formula" data-value="4(5 g+33)-20 g-132=0"><span
Q30: Solve the problem.<br>-One side of a
Q31: Solve the equation using the addition
Q32: Solve using the multiplication principle.<br>- <span
Q33: Solve using the multiplication principle.<br>- <span