Multiple Choice
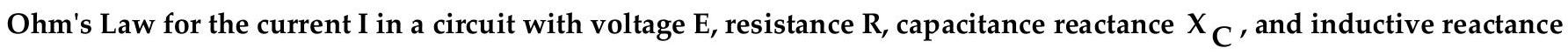 is . . Use this law to solve the problem.
is . . Use this law to solve the problem.
-Find if , and .
A)
B)
C)
D)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q298: Simplify the radical. Assume that all
Q299: Solve the problem. Give the answer
Q300: Explain how to evaluate <span
Q301: Write the fraction in lowest terms.<br>-
Q302: Choose the one alternative that best
Q304: How many real square roots does any
Q305: Choose the one alternative that best
Q306: (3i) (-2i)<br>A) -5<br>B) 6<br>C) -6<br>D) 5
Q307: Simplify the root.<br>- <span class="ql-formula" data-value="-\sqrt[3]{x^{21}}"><span
Q308: Choose the one alternative that best