Multiple Choice
Graph the function defined by a radical expression.
- 
A) 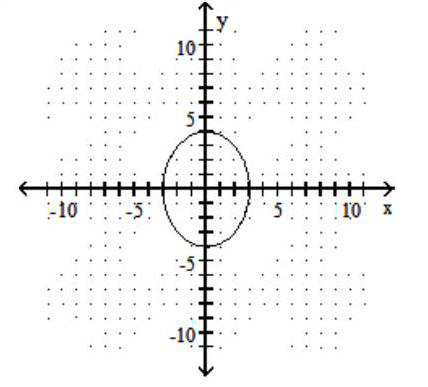
B) 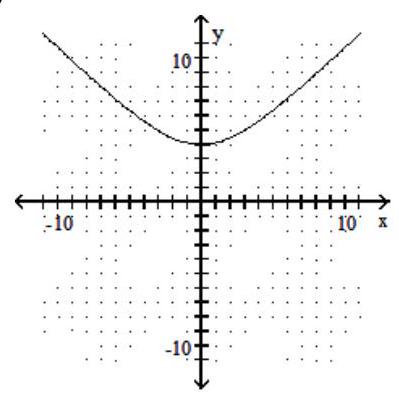
C) 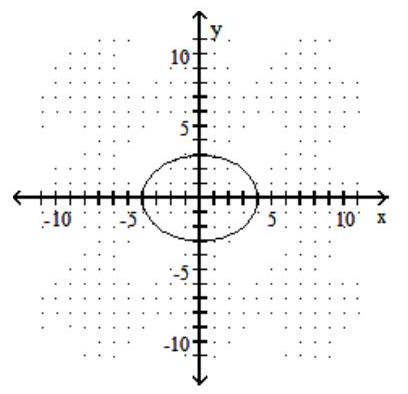
D) 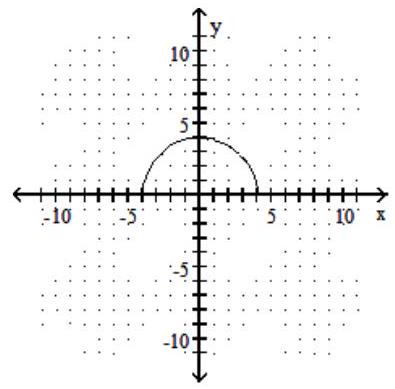
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q215: Solve the system by the elimination
Q216: Solve the nonlinear system.<br>- <span class="ql-formula"
Q217: Graph the rational function.<br>-f(x) =
Q218: Graph the system of inequalities.<br>- <span
Q219: Describe the graph of the solution
Q221: Solve the system by the substitution
Q222: Which one of the following is
Q223: Solve the system by the elimination
Q224: The equation of a semicircle that
Q225: Identify the graph of the equation