Multiple Choice
Solve the inequality. Give the solution set in both interval and graph forms.
- 
A) 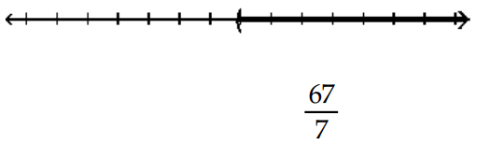
B) 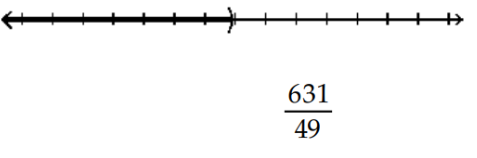
C) 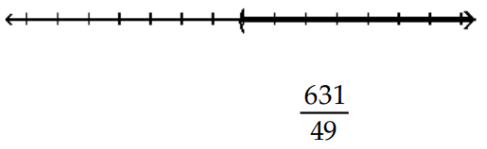
D) 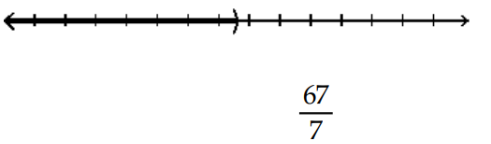
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q249: Decide whether the equation is conditional,
Q250: Solve the problem.<br>-Bert is 27.5 kilometers away
Q251: Which of the following is not
Q252: Solve the given equation or inequality.
Q253: Decide whether the equation is conditional,
Q255: Solve the inequality and graph the
Q256: Decide whether the equation is conditional,
Q257: Express the set in the simplest
Q258: Solve the equation.<br>- <span class="ql-formula" data-value="\frac{r+6}{5}=\frac{r+8}{7}"><span
Q259: For the compound inequality, decide whether