Solved

Assume That F Is a Function Whose Domain Is the Interval

Question 94

Essay

Assume that f is a function whose domain is the interval
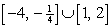
Assume that f is a function whose domain is the interval , whose range is the interval , and whose graph is the figure below. For g(x) = f(x - 2), A) find the domain of g. B) find the range of g. C) sketch the graph of g.
, whose range is the interval
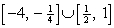Assume that f is a function whose domain is the interval , whose range is the interval , and whose graph is the figure below. For g(x) = f(x - 2), A) find the domain of g. B) find the range of g. C) sketch the graph of g. , and whose graph is the figure below. For g(x) = f(x - 2),
Assume that f is a function whose domain is the interval , whose range is the interval , and whose graph is the figure below. For g(x) = f(x - 2), A) find the domain of g. B) find the range of g. C) sketch the graph of g.

A) find the domain of g.
B) find the range of g.
C) sketch the graph of g.

Correct Answer:

verifed

Verified

Part A:
blured image ...

View Answer

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q89: Let f(x) = x<sup>2</sup> - x<sup>3</sup> with

Q90: Assume that f is a function whose

Q91: Suppose <br> <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB10659/.jpg" alt=" Suppose

Q92: Let f(x) = x<sup>2</sup> - x<sup>3</sup> with

Q93: Choose the composite of functions that would

Q95: Assume that <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB10659/.jpg" alt="Assume that

Q96: Every odd function is one-to-one.

Q97: Suppose <br> <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB10659/.jpg" alt="Suppose

Q98: Consider the function f whose graph is

Q99: Let f(x) = x<sup>2</sup> - x<sup>3</sup> with