Multiple Choice
Find the standard form of the ellipse with the following equation.
1x2 + 9y2 + 8x + 90y = -232
A) 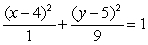
B) 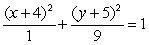
C) 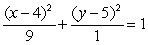
D) 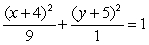
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q14: If the xy-coordinate axes are rotated 45°,
Q15: For the polar equation, (a) Identify the
Q16: Match the equation to the parabola. <img
Q17: Identify the conic section given by the
Q18: Find the equation of the ellipse with
Q20: Graph the second-degree equation. (Hint: Transform the
Q21: Find the standard form of the equation
Q22: Find the standard form of the equation
Q23: Graph the nonlinear inequality.<br> <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB10663/.jpg" alt="Graph
Q24: Identify the conic (parabola, ellipse, or hyperbola)