Solved

Use Row Operations to Transform the Matrix to Reduced Row-Echelon

Question 156

Multiple Choice

Use row operations to transform the matrix to reduced row-echelon form. Use row operations to transform the matrix to reduced row-echelon form. A) B) C) D)


A) Use row operations to transform the matrix to reduced row-echelon form. A) B) C) D)
B) Use row operations to transform the matrix to reduced row-echelon form. A) B) C) D)
C) Use row operations to transform the matrix to reduced row-echelon form. A) B) C) D)
D) Use row operations to transform the matrix to reduced row-echelon form. 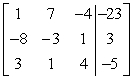A) 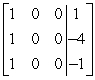B) C) 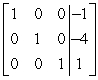D)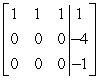

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q151: Apply the matrix algebra to solve the

Q152: Write the partial fraction decomposition for the

Q153: Perform the indicated operations for the expression,

Q154: Solve for the indicated variable. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB10663/.jpg"

Q155: Find the partial-fraction decomposition for the rational

Q157: Solve the system of linear equations by

Q158: Solve the system of linear equations by

Q159: Calculate AB if <br> <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB10663/.jpg" alt="Calculate

Q160: Find the partial-fraction decomposition for the rational

Q161: Match the graph to the linear inequality.