Solved

Find the Result of the Expression Using De Moivre's Theorem

Question 4

Multiple Choice

Find the result of the expression using De Moivre's theorem. Write the answer in rectangular form. Find the result of the expression using De Moivre's theorem. Write the answer in rectangular form. A) B) C) D)


A) Find the result of the expression using De Moivre's theorem. Write the answer in rectangular form. A) B) C) D)
B) Find the result of the expression using De Moivre's theorem. Write the answer in rectangular form. A) B) C) D)
C) Find the result of the expression using De Moivre's theorem. Write the answer in rectangular form. A) B) C) D)
D) Find the result of the expression using De Moivre's theorem. Write the answer in rectangular form. 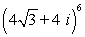A) 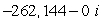B) 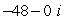C) 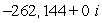D)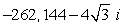

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q1: Find the angle (round to the nearest

Q2: Find the product, z<sub>1</sub>z<sub>2</sub> in rectangular form.<br>

Q3: Use a calculator to express the complex

Q5: Use a calculator to express the complex

Q6: Convert the point to exact rectangular coordinates.<br>

Q7: Find all nth roots of z. Write

Q8: Use a calculator to express the complex

Q9: Find the quotient,<br><img src="https://d2lvgg3v3hfg70.cloudfront.net/TB10663/.jpg" alt="Find the quotient,

Q10: To slide a crate across the floor,

Q11: Find all nth roots of z. Write