Height of a Sequoia Tree

Short Answer

Height of a sequoia tree. Sequoias are among the longest living trees in the world. They can grow to a maximum height of 311 ft and can live up to 3,200 years. A park ranger wants to determine the height of a sequoia tree without having to climb to the top of it. He measures the length of the tree's shadow and determines the angle of elevation from the tip of the shadow to the top of the tree. Using this information and a trigonometric function, the park ranger can calculate the height of the tree. What is the height of a tree if its shadow is 253 ft long and the angle of elevation is 43°? Round your answer to one decimal place.
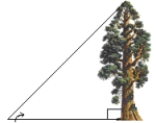43° 253 ft