In the Situation Shown in Figure T2 $0.021 U$ If We Multiply

Multiple Choice

In the situation shown in figure T2.5c, the width of the bell curve at half its peak value is $0.021 U$ . If we multiply $N_{A}$ , $N_{B}$ , and $U$ by a factor of 100 , then the peak's width (as you can check) is about $0.0021 U$ . Suppose that we increase each solid's $N$ and the system's total energy by another factor of $10^{18}$ to create solids containing $1 / 6$ of a mole of atoms (still pretty small objects by everyday standards) . Assuming that the trend continues, what will be the approximate width of the combined system's probability bell curve as a fraction of 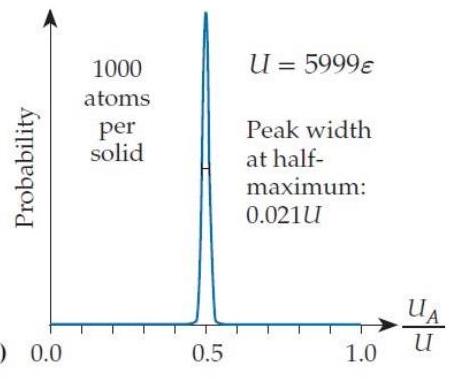$U$ ?

A) $2 \times 10^{-20}$
(c) 0.0
B) $2 \times 10^{-22}$
Figure T2.5
C) $2 \times 10^{-10}$
D) $\mathbf{2} \times \mathbf{1 0}^{-12}$
E) $2 \times 10^{-40}$
F) $2 \times 10^{-42}$
$\mathrm{T}$ . Some other factor (specify) .