Solve the Problem $x+w=700+400$ Or $x+w=1100$ by Writing an Equation Representing the Traffic Entering and Encountered

Multiple Choice

Solve the problem.
-During rush hours, substantial traffic congestion is encountered at the intersections shown in the figure. The arrows indicate one-way streets. As the figure shows, 400 cars per hour come down P Street to intersection A, and 700 cars per hour come down 5 th Street to intersection A. x of these cars leave A on P Street and w cars leave A on 5th Street.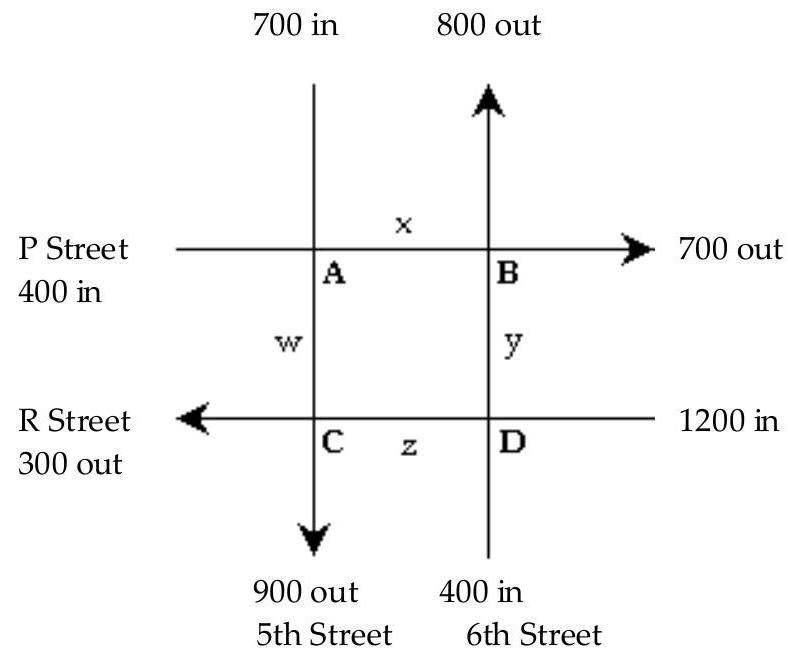
The number of cars entering intersection A must equal the number leaving, so that $x+w=700+400$ or $x+w=1100$ . By writing an equation representing the traffic entering and leaving each of the intersections A, B, C, and D, obtain a system of four equations. Solve the system using $\mathrm{W}$ as the parameter and use your answer to determine the largest and smallest possible values for the number of cars leaving intersection $\mathrm{D}$ on $\mathrm{R}$ Street.

A) $1200 ; 100$
B) $1100 ; 0$
C) $1200 ; 0$
D) $1100 ; 100$