Multiple Choice
Sketch the graph and show all local extrema and inflection points.
- 
A) 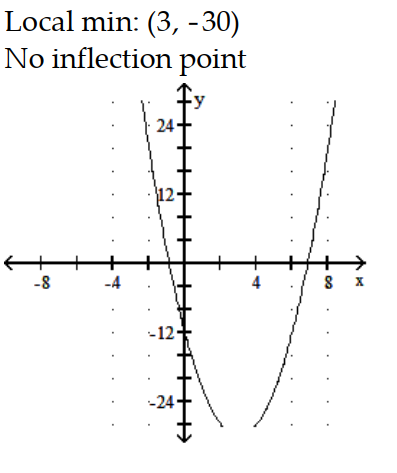
B) 
C) 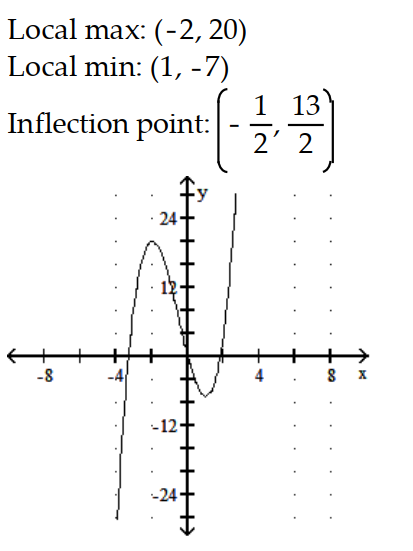
D) 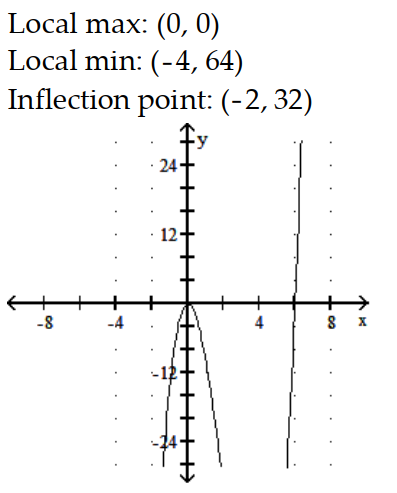
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q189: Solve the problem.<br>-Find the acceleration function
Q190: Evaluate <span class="ql-formula" data-value="\mathrm{f}^{\prime \prime}(\mathrm{c})"><span
Q191: The rule of the derivative of
Q192: Find the largest open interval where
Q193: Use the first derivative test to
Q195: Find the largest open intervals where
Q196: Find the location of the indicated
Q197: Find the location and value of
Q198: Solve the problem.<br>-A container, in the
Q199: Use calculus and a graphing calculator