The Practice of Making Confidence Intervals of

Multiple Choice

The practice of making confidence intervals of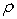
is recommended because

A) it is more accurate than hypothesis testing
B) it does not require the assumption of a normal bivariate distribution
C) it calls attention more directly to the influence of sampling variation on r
D) it takes better account of the number of degrees of freedom involved