The Manager of an Ice Cream Company Wants a Better

Short Answer

The manager of an ice cream company wants a better basis for deciding how much ice cream to make each evening. He would like to be able to predict the amount of ice cream sold at his retail outlets on any day from the temperature forecast the evening before. He records both the evening temperature forecast (X) and the number of five-gallon containers of ice cream sold the next day (Y) over a considerable period in the late spring and early summer. The following results are obtained:

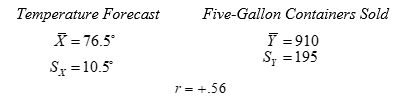
(a) Write the regression equation for predicting Y from X; simplify; and compute the standard error of prediction.
(b)Suppose the temperature forecast is for 96°. On what proportion of following days would he expect to sell over 1300 containers of ice cream?
(c)Suppose the forecast is for 50° and he plans to make 800 containers. For what proportion of the following days would this be too much ice cream?
(d)The regression equation is based on data gathered in the late spring and early summer. Will it "work" in midsummer, or in early fall?