Solved

Use the Following

Question 2

Short Answer

Use the following
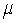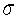Heights of 10-year-old girls (5th graders) follow an approximately normal distribution with mean Use the following Heights of 10-year-old girls (5th graders) follow an approximately normal distribution with mean = 54.4 inches and standard deviation of = 2.7 inches. -What proportion of 10-year-old girls are taller than 60 inches (5 feet)? Report your answer with three decimal places. = 54.4 inches and standard deviation of Use the following Heights of 10-year-old girls (5th graders) follow an approximately normal distribution with mean = 54.4 inches and standard deviation of = 2.7 inches. -What proportion of 10-year-old girls are taller than 60 inches (5 feet)? Report your answer with three decimal places. = 2.7 inches.
-What proportion of 10-year-old girls are taller than 60 inches (5 feet)? Report your answer with three decimal places.

Correct Answer:

verifed

Verified

Related Questions

Q1: Use the following <br>Use the provided density

Q3: Use the following <br>Heights of 10-year-old girls

Q4: Use the following <br>In the following, convert

Q5: Use the following <br>A set of hypotheses,

Q6: Use the following<br>Find the z* values based

Q7: Use the following <br>Robins are common birds

Q8: Use the following <br>Robins are common birds

Q9: Use the following<br>It is generally believed that

Q10: Use the following<br>There are 24 students enrolled

Q11: Use the following<br>Find the z* values based