Solved

Consider the Following Data β\beta 1 = 0 Versus H1 β\beta 1 ≠\neq

Question 22

Short Answer

Consider the following data.
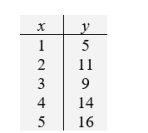
Consider the following data. A) Calculate the least squares estimate . B) Calculate the least squares estimate . C) Estimate the error variance . D) Test H<sub>0</sub>: \beta <sub>1</sub> = 0 versus H<sub>1</sub>: \beta <sub>1</sub> \neq 0 with \alpha = 0.05. Answer H<sub>0</sub> is rejected at \alpha = 0.05 or H<sub>0</sub> is not rejected at \alpha = 0.05 . E) Estimate the expected y value corresponding to x = 3. F) Give a 90% confidence interval for the expected y value at x = 3. Round your answer to two decimal places. 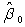Consider the following data. A) Calculate the least squares estimate . B) Calculate the least squares estimate . C) Estimate the error variance . D) Test H<sub>0</sub>: \beta <sub>1</sub> = 0 versus H<sub>1</sub>: \beta <sub>1</sub> \neq 0 with \alpha = 0.05. Answer H<sub>0</sub> is rejected at \alpha = 0.05 or H<sub>0</sub> is not rejected at \alpha = 0.05 . E) Estimate the expected y value corresponding to x = 3. F) Give a 90% confidence interval for the expected y value at x = 3. Round your answer to two decimal places.
A) Calculate the least squares estimate .
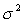
Consider the following data. A) Calculate the least squares estimate . B) Calculate the least squares estimate . C) Estimate the error variance . D) Test H<sub>0</sub>: \beta <sub>1</sub> = 0 versus H<sub>1</sub>: \beta <sub>1</sub> \neq 0 with \alpha = 0.05. Answer H<sub>0</sub> is rejected at \alpha = 0.05 or H<sub>0</sub> is not rejected at \alpha = 0.05 . E) Estimate the expected y value corresponding to x = 3. F) Give a 90% confidence interval for the expected y value at x = 3. Round your answer to two decimal places.
B) Calculate the least squares estimate .
Consider the following data. A) Calculate the least squares estimate . B) Calculate the least squares estimate . C) Estimate the error variance . D) Test H<sub>0</sub>: \beta <sub>1</sub> = 0 versus H<sub>1</sub>: \beta <sub>1</sub> \neq 0 with \alpha = 0.05. Answer H<sub>0</sub> is rejected at \alpha = 0.05 or H<sub>0</sub> is not rejected at \alpha = 0.05 . E) Estimate the expected y value corresponding to x = 3. F) Give a 90% confidence interval for the expected y value at x = 3. Round your answer to two decimal places.
C) Estimate the error variance .
Consider the following data. A) Calculate the least squares estimate . B) Calculate the least squares estimate . C) Estimate the error variance . D) Test H<sub>0</sub>: \beta <sub>1</sub> = 0 versus H<sub>1</sub>: \beta <sub>1</sub> \neq 0 with \alpha = 0.05. Answer H<sub>0</sub> is rejected at \alpha = 0.05 or H<sub>0</sub> is not rejected at \alpha = 0.05 . E) Estimate the expected y value corresponding to x = 3. F) Give a 90% confidence interval for the expected y value at x = 3. Round your answer to two decimal places.
D) Test H0: β\beta 1 = 0 versus H1: β\beta 1 ≠\neq 0 with α\alpha = 0.05. Answer "H0 is rejected at α\alpha = 0.05" or "H0 is not rejected at α\alpha = 0.05".
E) Estimate the expected y value corresponding to x = 3.
F) Give a 90% confidence interval for the expected y value at x = 3. Round your answer to two decimal places.

Correct Answer:

verifed

Verified

Part A: 2.5
Part B: 3.5
Part C...

View Answer

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q17: Which of the following statements is

Q18: Consider the line y = -6 +

Q19: Consider the data set<br> <br> <img

Q20: Consider the following data set.<br> <img

Q21: Suppose that n = 21,

Q23: An internet site lists the prices, y,

Q24: One measure of the development of

Q25: Calculate the correlation coefficient between the number

Q26: An advertising company collected data on

Q27: Consider the following data set<br> <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB10841/.jpg"