Exhibit 6.2 The Following Questions Pertain to the Problem, Formulation, and Spreadsheet

Essay

Exhibit 6.2
The following questions pertain to the problem, formulation, and spreadsheet implementation below.
A certain military deployment requires supplies delivered to four locations. These deliveries come from one of three ports. Logistics planners wish to deliver the supplies in an efficient manner, in this case by minimizing total ton-miles. The port-destination data, along with destination demand is provided in the following table. The ports are supplied by one of two supply ships. These ships travel to a particular port where their supplies are off-loaded and shipped to the requesting destinations. Ship S1 carries 1200 tones of supplies while Ship S2 carries 1120 tons of supplies. These ships can only go to a single port and each port can only accommodate one ship. Assume the costs for a ship to travel to a port are not part of the objective function.
The following is the ILP formulation and a spreadsheet model for the problem.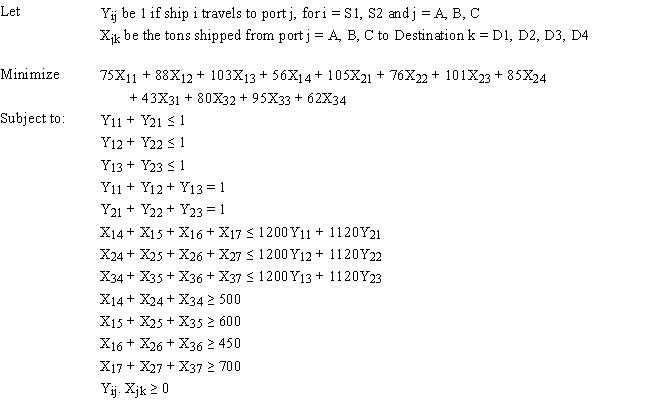
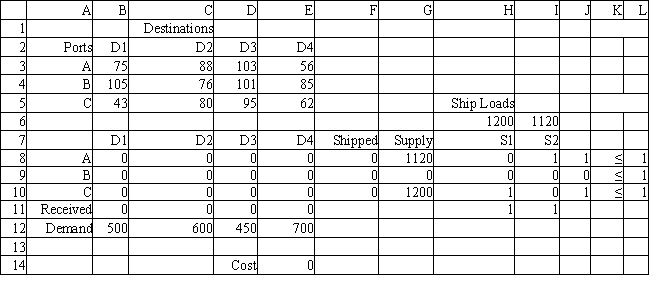
-Refer to Exhibit 6.2. What formula would go into cells B11:E11 and cells F8:F10?