Multiple Choice
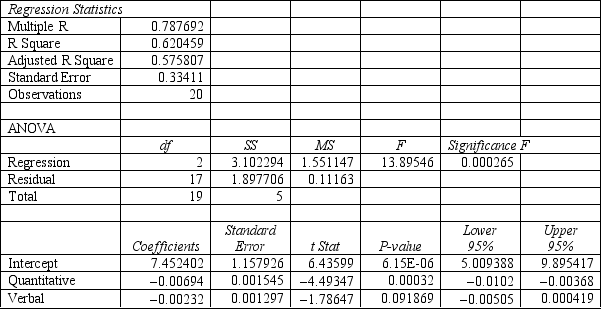
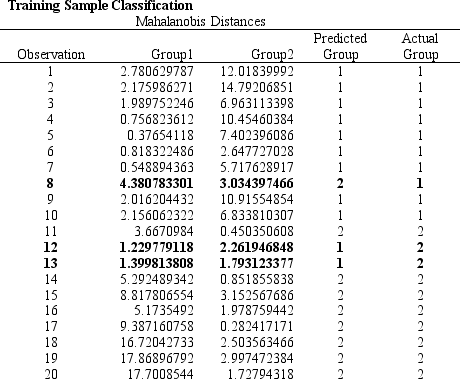
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2) .
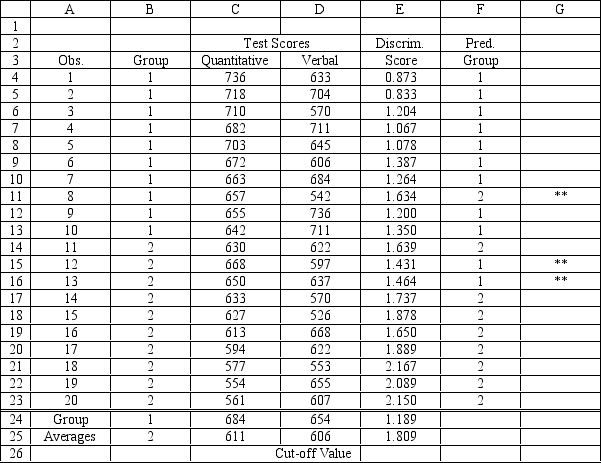


-Refer to Exhibit 10.1. The straight line distance between two points (X1, Y1) and (X2, Y2) is calculated as
A) X1 - Y1 + X2 -Y2
B) (X1 - X2) 2 + (Y1 - Y2) 2
C) 
D) 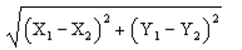
Correct Answer:

Verified
Correct Answer:
Verified
Q29: Multiple discriminant analysis moves away from a
Q31: In a two-group discriminant analysis problem using
Q32: The discriminant score is denoted by<br>A)<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5443/.jpg"
Q51: In discriminant analysis the averages for the
Q53: Exhibit 10.2<br>The following questions are based on
Q61: Discriminant analysis (DA) differs from most other
Q90: Exhibit 10.1<br>The following questions are based on
Q104: Exhibit 10.1<br>The following questions are based on
Q115: Exhibit 10.2<br>The following questions are based on
Q124: Exhibit 10.6<br>The information below is used for