Solved

What Is the Probability That It Will Take Less Than μ\mu

Question 5

Multiple Choice

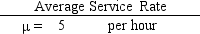
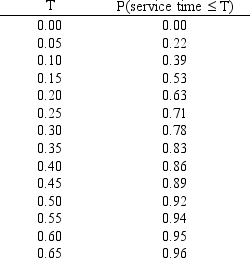
What is the probability that it will take less than or equal to 0.25 hours to service any call based on the following exponential probability distribution with rate μ\mu = 5? What is the probability that it will take less than or equal to 0.25 hours to service any call based on the following exponential probability distribution with rate \mu = 5? A) 0.00 B) 0.71 C) 0.92 D) 1.00 What is the probability that it will take less than or equal to 0.25 hours to service any call based on the following exponential probability distribution with rate \mu = 5? A) 0.00 B) 0.71 C) 0.92 D) 1.00


A) 0.00
B) 0.71
C) 0.92
D) 1.00

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q6: The M/D/1 model results can be

Q10: Project 13.1 - Internet Sales, Inc.Internet Sales,

Q16: Exhibit 12.5<br>The following questions use the information

Q17: Exhibit 13.2<br>The following questions refer to the

Q23: A grocery clerk can serve 20 customers

Q35: Exhibit 13.5<br>The following questions refer to the

Q51: Exhibit 13.1<br>The following questions are based on

Q78: Exhibit 13.3<br>The following questions refer to the

Q81: Exhibit 13.4<br>The following questions refer to the

Q86: Exhibit 13.4<br>The following questions refer to the