Given the Following Null and Alternative Hypotheses H₀ : μ₁

Multiple Choice

Given the following null and alternative hypotheses H₀ : μ₁ ≥ μ₂
H_A : μ₁ < μ₂
Together with the following sample information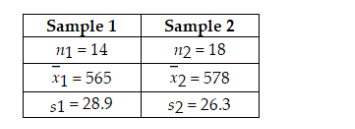
Assuming that the populations are normally distributed with equal variances,test at the 0.05 level of significance whether you would reject the null hypothesis based on the sample information.Use the test statistic approach.

A) Because the calculated value of t = -2.145 is less than the critical value of t = -1.6973,reject the null hypothesis.Based on these sample data,at the α = 0.05 level of significance there is sufficient evidence to conclude that the mean for population 1 is less than the mean for population 2.
B) Because the calculated value of t = -1.814 is less than the critical value of t = -1.6973,reject the null hypothesis.Based on these sample data,at the α = 0.05 level of significance there is sufficient evidence to conclude that the mean for population 1 is less than the mean for population 2.
C) Because the calculated value of t = -1.329 is not less than the critical value of t = -1.6973,do not reject the null hypothesis.Based on these sample data,at the α = 0.05 level of significance there is not sufficient evidence to conclude that the mean for population 1 is less than the mean for population 2.
D) Because the calculated value of t = -1.415 is not less than the critical value of t = -1.6973,do not reject the null hypothesis.Based on these sample data,at the α = 0.05 level of significance there is not sufficient evidence to conclude that the mean for population 1 is less than the mean for population 2.