The Certainty Equivalent of a Gamble Is Defined to Be

Essay

The certainty equivalent of a gamble is defined to be the amount of money which, if you were promised it with certainty, would be indifferent to the gamble.
a. If an expected utility maximizer has a von Neuman-Morgenstern utility function U(W) = W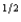
(where W is wealth) and if the probability of events 1 and 2 are both , write a formula for the certainty equivalent of a gamble that gives you x if event 1 happens and y if event 2 happens.
b. Generalize your formula in part (a) to the case where the probability of event 1 is p and the probability of event 2 is 1 - p.
c. Generalize the formula in part (a) to the case where U(W) = W^a for a > 0.