(See Problem 2

Multiple Choice

(See Problem 2.) Willy's only source of wealth is his chocolate factory. He has the utility function 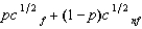, where p is the probability of a flood, 1 - p is the probability of no flood, and c_f and c_nf are his wealth contingent on a flood and on no flood, respectively. The probability of a flood is p = 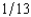. The value of Willy's factory is $500,000 if there is no flood and 0 if there is a flood. Willy can buy insurance where if he buys $x worth of insurance, he must pay the insurance company $ 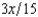whether there is a flood or not, but he gets back $x from the company if there is a flood. Willy should buy

A) no insurance since the cost per dollar of insurance exceeds the probability of a flood.
B) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there is no flood.
C) enough insurance so that if there is a flood, after he collects his insurance, his wealth will be the same whether there is a flood or not.
D) .enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there is no flood.
E) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there is no flood