(See Problem 11

Multiple Choice

(See Problem 11.) Albert's expected utility function is 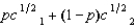, where p is the probability that he consumes c₁ and 1 - p is the probability that he consumes c₂. Albert is offered a choice between getting a sure payment of $Z or a lottery in which he receives $400 with probability .30 or $2,500 with probability .70. Albert will choose the sure payment if

A) Z > 2,090.50 and the lottery if Z < 2,090.50.
B) Z > 1,040.50 and the lottery if Z < 1,040.50.
C) Z > 2,500 and the lottery if Z < 2,500.
D) Z > 1,681 and the lottery if Z < 1,681.
E) Z > 1,870 and the lottery if Z < 1,870.