Solved

Let F and G Be Real-Valued Functions

Question 24

Short Answer

Let f and g be real-valued functions. Assume that f and g are nonnegative, that is, for all real numbers
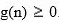Let f and g be real-valued functions. Assume that f and g are nonnegative, that is, for all real numbers and We say that is of g(n). written if there exist positive constants c and such that For all and Let f and g be real-valued functions. Assume that f and g are nonnegative, that is, for all real numbers and We say that is of g(n). written if there exist positive constants c and such that For all We say that Let f and g be real-valued functions. Assume that f and g are nonnegative, that is, for all real numbers and We say that is of g(n). written if there exist positive constants c and such that For all is of g(n). written Let f and g be real-valued functions. Assume that f and g are nonnegative, that is, for all real numbers and We say that is of g(n). written if there exist positive constants c and such that For all
if there exist positive constants c and Let f and g be real-valued functions. Assume that f and g are nonnegative, that is, for all real numbers and We say that is of g(n). written if there exist positive constants c and such that For all such that Let f and g be real-valued functions. Assume that f and g are nonnegative, that is, for all real numbers and We say that is of g(n). written if there exist positive constants c and such that For all For all Let f and g be real-valued functions. Assume that f and g are nonnegative, that is, for all real numbers and We say that is of g(n). written 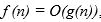if there exist positive constants c and 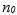such that 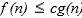For all

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q4: A sequence of branches in a comparison

Q13: Let f be a function of n.By

Q14: We can trace the execution of a

Q25: A sequential search of an n-element list

Q26: If a list of eight elements is

Q27: Consider the following list:int list[] = {4,

Q27: A sequential search of an n-element list

Q28: The quick sort algorithm uses the _

Q31: The _ search algorithm is the optimal

Q40: With insertion sort, the variable firstOutOfOrder is