A Campaign Manager for a Political Candidate Must Arrange the Shipment

Multiple Choice

A campaign manager for a political candidate must arrange the shipment of 150 cartons of campaign buttons from three button producers to three campaign headquarters. The supplies and demands, and the per-carton transportation costs, are shown below: 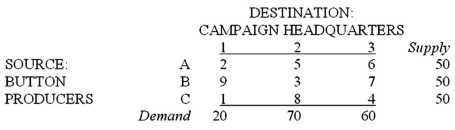Which of the following is an objective function for the problem?

A)
$\operatorname { Min } 50 \mathrm { X } _ { 11 } + 50 \mathrm { X } _ { 12 } + 50 \mathrm { X } _ { 13 } + 20 \mathrm { X } _ { 31 } + 70 \mathrm { X } _ { 32 } + 60 \mathrm { X } _ { 33 }$
B)
$\operatorname { Min } 2 X _ { 11 } + 5 X _ { 12 } + 6 X _ { 13 } + 9 X _ { 21 } + 3 X _ { 22 } + 7 X _ { 23 } + X _ { 31 } + 8 X _ { 32 } + 4 X _ { 33 }$
C)
$\operatorname { Max } 2 X _ { 11 } + 5 X _ { 12 } + 6 X _ { 13 } + 9 X _ { 21 } + 3 X _ { 22 } + 7 X _ { 23 } + X _ { 31 } + 8 X _ { 32 } + 4 X _ { 33 }$
D)
$\operatorname { Max } 20 \mathrm { X } _ { 11 } + 70 \mathrm { X } _ { 12 } + 60 \mathrm { X } _ { 13 } + 50 \mathrm { X } _ { 31 } + 50 \mathrm { X } _ { 32 } + 50 \mathrm { X } _ { 33 }$
E) None of the choices.