Southside College Has Modeled Its Student Loan Program as a Markov

Short Answer

Southside College has modeled its student loan program as a Markov process.Each year a student with a prior loan borrows again,defers repayment for a year,makes payments,pays the loan balance in full,or defaults on repayment.The transition matrix is as follows: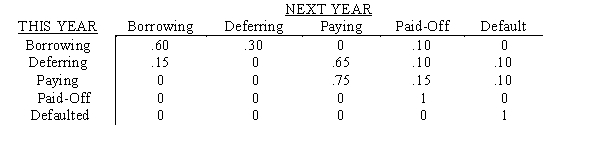
a. If currently a student is making payments on his/her loan, what is the probability the loan will be paid in full eventually?
b. Is the probability of eventually defaulting greater for a student who is currently borrowing more or a student who is making payments?
c. What is the probability a student who is borrowing this year will repay the loan balance in full in two years or less?