Solved

The Amount of Money That Maria Earns in a Week

Question 84

Multiple Choice

The amount of money that Maria earns in a week is a random variable,X,with a mean of $900 and a standard deviation of The amount of money that Maria earns in a week is a random variable,X,with a mean of $900 and a standard deviation of .The amount of money that Daniel earns in a week is a random variable,Y,with a mean of $800 and a standard deviation of .The difference,X - Y,between Maria's weekly income and Daniel's weekly income is a random variable with a mean of $900 - $800 = $100.If the incomes are independent of one another,which of the following shows the correct method for calculating the standard deviation of the random variable X - Y? A) SD(X - Y) = Var(X - Y) = Var(X) + Var(Y) = + B) SD(X - Y) = = = C) SD(X - Y) = SD(X) + SD(Y) = + D) SD(X - Y) = SD(X) - SD(Y) = - E) SD(X - Y) = = =
.The amount of money that Daniel earns in a week is a random variable,Y,with a mean of $800 and a standard deviation of The amount of money that Maria earns in a week is a random variable,X,with a mean of $900 and a standard deviation of .The amount of money that Daniel earns in a week is a random variable,Y,with a mean of $800 and a standard deviation of .The difference,X - Y,between Maria's weekly income and Daniel's weekly income is a random variable with a mean of $900 - $800 = $100.If the incomes are independent of one another,which of the following shows the correct method for calculating the standard deviation of the random variable X - Y? A) SD(X - Y) = Var(X - Y) = Var(X) + Var(Y) = + B) SD(X - Y) = = = C) SD(X - Y) = SD(X) + SD(Y) = + D) SD(X - Y) = SD(X) - SD(Y) = - E) SD(X - Y) = = =
.The difference,X - Y,between Maria's weekly income and Daniel's weekly income is a random variable with a mean of $900 - $800 = $100.If the incomes are independent of one another,which of the following shows the correct method for calculating the standard deviation of the random variable X - Y?


A) SD(X - Y) = Var(X - Y) = Var(X) + Var(Y) =
The amount of money that Maria earns in a week is a random variable,X,with a mean of $900 and a standard deviation of .The amount of money that Daniel earns in a week is a random variable,Y,with a mean of $800 and a standard deviation of .The difference,X - Y,between Maria's weekly income and Daniel's weekly income is a random variable with a mean of $900 - $800 = $100.If the incomes are independent of one another,which of the following shows the correct method for calculating the standard deviation of the random variable X - Y? A) SD(X - Y) = Var(X - Y) = Var(X) + Var(Y) = + B) SD(X - Y) = = = C) SD(X - Y) = SD(X) + SD(Y) = + D) SD(X - Y) = SD(X) - SD(Y) = - E) SD(X - Y) = = =
+
The amount of money that Maria earns in a week is a random variable,X,with a mean of $900 and a standard deviation of .The amount of money that Daniel earns in a week is a random variable,Y,with a mean of $800 and a standard deviation of .The difference,X - Y,between Maria's weekly income and Daniel's weekly income is a random variable with a mean of $900 - $800 = $100.If the incomes are independent of one another,which of the following shows the correct method for calculating the standard deviation of the random variable X - Y? A) SD(X - Y) = Var(X - Y) = Var(X) + Var(Y) = + B) SD(X - Y) = = = C) SD(X - Y) = SD(X) + SD(Y) = + D) SD(X - Y) = SD(X) - SD(Y) = - E) SD(X - Y) = = =
B) SD(X - Y) =
The amount of money that Maria earns in a week is a random variable,X,with a mean of $900 and a standard deviation of .The amount of money that Daniel earns in a week is a random variable,Y,with a mean of $800 and a standard deviation of .The difference,X - Y,between Maria's weekly income and Daniel's weekly income is a random variable with a mean of $900 - $800 = $100.If the incomes are independent of one another,which of the following shows the correct method for calculating the standard deviation of the random variable X - Y? A) SD(X - Y) = Var(X - Y) = Var(X) + Var(Y) = + B) SD(X - Y) = = = C) SD(X - Y) = SD(X) + SD(Y) = + D) SD(X - Y) = SD(X) - SD(Y) = - E) SD(X - Y) = = =
=
The amount of money that Maria earns in a week is a random variable,X,with a mean of $900 and a standard deviation of .The amount of money that Daniel earns in a week is a random variable,Y,with a mean of $800 and a standard deviation of .The difference,X - Y,between Maria's weekly income and Daniel's weekly income is a random variable with a mean of $900 - $800 = $100.If the incomes are independent of one another,which of the following shows the correct method for calculating the standard deviation of the random variable X - Y? A) SD(X - Y) = Var(X - Y) = Var(X) + Var(Y) = + B) SD(X - Y) = = = C) SD(X - Y) = SD(X) + SD(Y) = + D) SD(X - Y) = SD(X) - SD(Y) = - E) SD(X - Y) = = =
=
The amount of money that Maria earns in a week is a random variable,X,with a mean of $900 and a standard deviation of .The amount of money that Daniel earns in a week is a random variable,Y,with a mean of $800 and a standard deviation of .The difference,X - Y,between Maria's weekly income and Daniel's weekly income is a random variable with a mean of $900 - $800 = $100.If the incomes are independent of one another,which of the following shows the correct method for calculating the standard deviation of the random variable X - Y? A) SD(X - Y) = Var(X - Y) = Var(X) + Var(Y) = + B) SD(X - Y) = = = C) SD(X - Y) = SD(X) + SD(Y) = + D) SD(X - Y) = SD(X) - SD(Y) = - E) SD(X - Y) = = =
C) SD(X - Y) = SD(X) + SD(Y) =
The amount of money that Maria earns in a week is a random variable,X,with a mean of $900 and a standard deviation of .The amount of money that Daniel earns in a week is a random variable,Y,with a mean of $800 and a standard deviation of .The difference,X - Y,between Maria's weekly income and Daniel's weekly income is a random variable with a mean of $900 - $800 = $100.If the incomes are independent of one another,which of the following shows the correct method for calculating the standard deviation of the random variable X - Y? A) SD(X - Y) = Var(X - Y) = Var(X) + Var(Y) = + B) SD(X - Y) = = = C) SD(X - Y) = SD(X) + SD(Y) = + D) SD(X - Y) = SD(X) - SD(Y) = - E) SD(X - Y) = = =
+
The amount of money that Maria earns in a week is a random variable,X,with a mean of $900 and a standard deviation of .The amount of money that Daniel earns in a week is a random variable,Y,with a mean of $800 and a standard deviation of .The difference,X - Y,between Maria's weekly income and Daniel's weekly income is a random variable with a mean of $900 - $800 = $100.If the incomes are independent of one another,which of the following shows the correct method for calculating the standard deviation of the random variable X - Y? A) SD(X - Y) = Var(X - Y) = Var(X) + Var(Y) = + B) SD(X - Y) = = = C) SD(X - Y) = SD(X) + SD(Y) = + D) SD(X - Y) = SD(X) - SD(Y) = - E) SD(X - Y) = = =
D) SD(X - Y) = SD(X) - SD(Y) =
The amount of money that Maria earns in a week is a random variable,X,with a mean of $900 and a standard deviation of .The amount of money that Daniel earns in a week is a random variable,Y,with a mean of $800 and a standard deviation of .The difference,X - Y,between Maria's weekly income and Daniel's weekly income is a random variable with a mean of $900 - $800 = $100.If the incomes are independent of one another,which of the following shows the correct method for calculating the standard deviation of the random variable X - Y? A) SD(X - Y) = Var(X - Y) = Var(X) + Var(Y) = + B) SD(X - Y) = = = C) SD(X - Y) = SD(X) + SD(Y) = + D) SD(X - Y) = SD(X) - SD(Y) = - E) SD(X - Y) = = =
-
The amount of money that Maria earns in a week is a random variable,X,with a mean of $900 and a standard deviation of .The amount of money that Daniel earns in a week is a random variable,Y,with a mean of $800 and a standard deviation of .The difference,X - Y,between Maria's weekly income and Daniel's weekly income is a random variable with a mean of $900 - $800 = $100.If the incomes are independent of one another,which of the following shows the correct method for calculating the standard deviation of the random variable X - Y? A) SD(X - Y) = Var(X - Y) = Var(X) + Var(Y) = + B) SD(X - Y) = = = C) SD(X - Y) = SD(X) + SD(Y) = + D) SD(X - Y) = SD(X) - SD(Y) = - E) SD(X - Y) = = =
E) SD(X - Y) =
The amount of money that Maria earns in a week is a random variable,X,with a mean of $900 and a standard deviation of .The amount of money that Daniel earns in a week is a random variable,Y,with a mean of $800 and a standard deviation of .The difference,X - Y,between Maria's weekly income and Daniel's weekly income is a random variable with a mean of $900 - $800 = $100.If the incomes are independent of one another,which of the following shows the correct method for calculating the standard deviation of the random variable X - Y? A) SD(X - Y) = Var(X - Y) = Var(X) + Var(Y) = + B) SD(X - Y) = = = C) SD(X - Y) = SD(X) + SD(Y) = + D) SD(X - Y) = SD(X) - SD(Y) = - E) SD(X - Y) = = =
=
The amount of money that Maria earns in a week is a random variable,X,with a mean of $900 and a standard deviation of .The amount of money that Daniel earns in a week is a random variable,Y,with a mean of $800 and a standard deviation of .The difference,X - Y,between Maria's weekly income and Daniel's weekly income is a random variable with a mean of $900 - $800 = $100.If the incomes are independent of one another,which of the following shows the correct method for calculating the standard deviation of the random variable X - Y? A) SD(X - Y) = Var(X - Y) = Var(X) + Var(Y) = + B) SD(X - Y) = = = C) SD(X - Y) = SD(X) + SD(Y) = + D) SD(X - Y) = SD(X) - SD(Y) = - E) SD(X - Y) = = =
=
The amount of money that Maria earns in a week is a random variable,X,with a mean of $900 and a standard deviation of 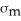.The amount of money that Daniel earns in a week is a random variable,Y,with a mean of $800 and a standard deviation of 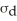.The difference,X - Y,between Maria's weekly income and Daniel's weekly income is a random variable with a mean of $900 - $800 = $100.If the incomes are independent of one another,which of the following shows the correct method for calculating the standard deviation of the random variable X - Y? 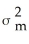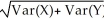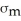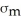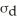A) SD(X - Y) = Var(X - Y) = Var(X) + Var(Y) = + B) SD(X - Y) = = = C) SD(X - Y) = SD(X) + SD(Y) = + D) SD(X - Y) = SD(X) - SD(Y) = - E) SD(X - Y) = = =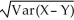

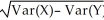
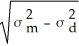
Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q80: A company is interviewing applicants for managerial

Q81: Janet is planning to rent a booth

Q83: A carnival game offers a $80 cash

Q85: Given independent random variables with means and

Q86: Sue Anne owns a medium-sized business.The probability

Q87: The number of golf balls ordered by

Q104: In a box of 8 batteries,5 are

Q169: You pick a card from a deck.If

Q176: A company sells light bulbs in packages

Q205: A company bids on two contracts.It anticipates