Solved

A Two-Sample Z-Test for Two Population Proportions Is to Be

Question 5

Multiple Choice

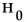
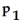
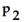
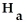
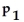
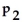
A two-sample z-test for two population proportions is to be performed using the P-value approach.The null hypothesis is A two-sample z-test for two population proportions is to be performed using the P-value approach.The null hypothesis is : = and the alternative is : ≠ .Use the given sample data to find the P-value for the hypothesis test.Give an interpretation of the p-value. -n<sub>1</sub> = 50 n<sub>2</sub> = 75 X<sub>1</sub> = 20 x<sub>2</sub> = 15 A) P-value = 0.0073;There is about a 0.73% chance that the two proportions are equal. B) P-value = 0.0073;If there is no difference in the proportions,there is about a 0.73% chance of seeing the observed difference or larger by natural sampling variation. C) P-value = 0.0037;If there is no difference in the proportions,there is a 0.37% chance of seeing the exact observed difference by natural sampling variation. D) P-value = 0.0146;If there is no difference in the proportions,there is about a 1.46% chance of seeing the observed difference or larger by natural sampling variation. E) P-value = 0.0146;There is about a 1.46% chance that the two proportions are equal.
: A two-sample z-test for two population proportions is to be performed using the P-value approach.The null hypothesis is : = and the alternative is : ≠ .Use the given sample data to find the P-value for the hypothesis test.Give an interpretation of the p-value. -n<sub>1</sub> = 50 n<sub>2</sub> = 75 X<sub>1</sub> = 20 x<sub>2</sub> = 15 A) P-value = 0.0073;There is about a 0.73% chance that the two proportions are equal. B) P-value = 0.0073;If there is no difference in the proportions,there is about a 0.73% chance of seeing the observed difference or larger by natural sampling variation. C) P-value = 0.0037;If there is no difference in the proportions,there is a 0.37% chance of seeing the exact observed difference by natural sampling variation. D) P-value = 0.0146;If there is no difference in the proportions,there is about a 1.46% chance of seeing the observed difference or larger by natural sampling variation. E) P-value = 0.0146;There is about a 1.46% chance that the two proportions are equal.
= A two-sample z-test for two population proportions is to be performed using the P-value approach.The null hypothesis is : = and the alternative is : ≠ .Use the given sample data to find the P-value for the hypothesis test.Give an interpretation of the p-value. -n<sub>1</sub> = 50 n<sub>2</sub> = 75 X<sub>1</sub> = 20 x<sub>2</sub> = 15 A) P-value = 0.0073;There is about a 0.73% chance that the two proportions are equal. B) P-value = 0.0073;If there is no difference in the proportions,there is about a 0.73% chance of seeing the observed difference or larger by natural sampling variation. C) P-value = 0.0037;If there is no difference in the proportions,there is a 0.37% chance of seeing the exact observed difference by natural sampling variation. D) P-value = 0.0146;If there is no difference in the proportions,there is about a 1.46% chance of seeing the observed difference or larger by natural sampling variation. E) P-value = 0.0146;There is about a 1.46% chance that the two proportions are equal.
and the alternative is A two-sample z-test for two population proportions is to be performed using the P-value approach.The null hypothesis is : = and the alternative is : ≠ .Use the given sample data to find the P-value for the hypothesis test.Give an interpretation of the p-value. -n<sub>1</sub> = 50 n<sub>2</sub> = 75 X<sub>1</sub> = 20 x<sub>2</sub> = 15 A) P-value = 0.0073;There is about a 0.73% chance that the two proportions are equal. B) P-value = 0.0073;If there is no difference in the proportions,there is about a 0.73% chance of seeing the observed difference or larger by natural sampling variation. C) P-value = 0.0037;If there is no difference in the proportions,there is a 0.37% chance of seeing the exact observed difference by natural sampling variation. D) P-value = 0.0146;If there is no difference in the proportions,there is about a 1.46% chance of seeing the observed difference or larger by natural sampling variation. E) P-value = 0.0146;There is about a 1.46% chance that the two proportions are equal.
: A two-sample z-test for two population proportions is to be performed using the P-value approach.The null hypothesis is : = and the alternative is : ≠ .Use the given sample data to find the P-value for the hypothesis test.Give an interpretation of the p-value. -n<sub>1</sub> = 50 n<sub>2</sub> = 75 X<sub>1</sub> = 20 x<sub>2</sub> = 15 A) P-value = 0.0073;There is about a 0.73% chance that the two proportions are equal. B) P-value = 0.0073;If there is no difference in the proportions,there is about a 0.73% chance of seeing the observed difference or larger by natural sampling variation. C) P-value = 0.0037;If there is no difference in the proportions,there is a 0.37% chance of seeing the exact observed difference by natural sampling variation. D) P-value = 0.0146;If there is no difference in the proportions,there is about a 1.46% chance of seeing the observed difference or larger by natural sampling variation. E) P-value = 0.0146;There is about a 1.46% chance that the two proportions are equal.
≠ A two-sample z-test for two population proportions is to be performed using the P-value approach.The null hypothesis is : = and the alternative is : ≠ .Use the given sample data to find the P-value for the hypothesis test.Give an interpretation of the p-value. -n<sub>1</sub> = 50 n<sub>2</sub> = 75 X<sub>1</sub> = 20 x<sub>2</sub> = 15 A) P-value = 0.0073;There is about a 0.73% chance that the two proportions are equal. B) P-value = 0.0073;If there is no difference in the proportions,there is about a 0.73% chance of seeing the observed difference or larger by natural sampling variation. C) P-value = 0.0037;If there is no difference in the proportions,there is a 0.37% chance of seeing the exact observed difference by natural sampling variation. D) P-value = 0.0146;If there is no difference in the proportions,there is about a 1.46% chance of seeing the observed difference or larger by natural sampling variation. E) P-value = 0.0146;There is about a 1.46% chance that the two proportions are equal.
.Use the given sample data to find the P-value for the hypothesis test.Give an interpretation of the p-value.
-n1 = 50 n2 = 75
X1 = 20 x2 = 15


A) P-value = 0.0073;There is about a 0.73% chance that the two proportions are equal.
B) P-value = 0.0073;If there is no difference in the proportions,there is about a 0.73% chance of seeing the observed difference or larger by natural sampling variation.
C) P-value = 0.0037;If there is no difference in the proportions,there is a 0.37% chance of seeing the exact observed difference by natural sampling variation.
D) P-value = 0.0146;If there is no difference in the proportions,there is about a 1.46% chance of seeing the observed difference or larger by natural sampling variation.
E) P-value = 0.0146;There is about a 1.46% chance that the two proportions are equal.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q1: A new manager started a program on

Q4: Suppose the proportion of first year students

Q6: A university found it retained 25 students

Q9: Suppose the proportion of women who follow

Q10: A new manager,hired at a large warehouse,was

Q15: A survey of randomly selected university students

Q20: You wish to construct a 95% confidence

Q24: A new manager,hired at a large warehouse,was

Q35: A marketing survey involves product recognition in

Q49: In a random sample of 300 Canadian