In the Past,the Mean Battery Life for a Certain Type

Multiple Choice

In the past,the mean battery life for a certain type of flashlight battery has been 9.5 hours.The manufacturer has introduced a change in the production method and wants to perform a hypothesis test to determine whether the mean battery life has increased as a result.The hypotheses are: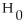
: μ = 9.5 hours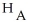
: μ > 9.5 hours
Explain the result of a Type II error.

A) The manufacturer will not decide the mean battery life is greater than 9.5 hours when in fact it is greater than 9.5 hours.
B) The manufacturer will decide the mean battery life is greater than 9.5 hours when in fact it is 9.5 hours.
C) The manufacturer will decide the mean battery life is greater than 9.5 hours when in fact it is greater than 9.5 hours.
D) The manufacturer will decide the mean battery life is 9.6 hours lower than it was prior to the change in the production method.
E) The manufacturer will decide the mean battery life is 8.1 hours greater than it was prior to the change in the production method.