The Index of Exposure to Radioactive Waste and the Cancer

Multiple Choice

The index of exposure to radioactive waste and the cancer mortality rates (deaths per 100,000) were recorded for nine different geographic regions.A 95% prediction interval for the cancer mortality rate of a region whose index of exposure is 5.79 is 133.0 to 203.4 deaths per 100,000.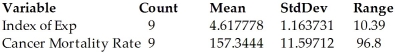
Dependent variable is: Cancer Mortality Rate
R-squared = 85.8%
S = 14.00993 with 9 - 2 = 7 degrees of freedom

A) Based on this regression,we are 95% confident that the index of exposure will increase between 133.0 and 203.4 for each unit increase in the cancer mortality rate over 5.79.
B) Based on this regression,we know that 95% of all random samples of regions will have a mean cancer mortality rate that is between 133.0 and 203.4 deaths per 100,000.
C) Based on this regression,we are 95% confident that a region with an index of exposure of 5.79 will have a cancer mortality rate that is between 133.0 and 203.4 deaths per 100,000.
D) Based on this regression,we are 95% confident that the mean cancer mortality rate will increase between 133.0 and 203.4 deaths per 100,000 for each unit increase in the index of exposure over 5.79.
E) Based on this regression,we are 95% confident that the mean cancer mortality rate for regions with an index of exposure of 5.79 will be between 133.0 and 203.4 deaths per 100,000.