Essay
Secure Strategies. Suppose two competitors, McGraw-Hill, Inc., and Pearson, PLC., each face an important strategic decision concerning whether or not they should boost promotion on new product introductions. McGraw-Hill can choose either row in the payoff matrix defined below, whereas Pearson can choose either column. For McGraw-Hill, the choice is either "boost promotion" or "hold promotion constant." For Pearson, the choices are the same. Notice that neither firm can unilaterally choose a given cell in the profit payoff matrix. The ultimate result of this one-shot, simultaneous-move game depends upon the choices made by both competitors. In this payoff matrix, the first number in each cell is the profit payoff to McGraw-Hill; the second number is the profit payoff to Pearson (in billions).

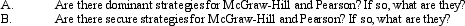
Correct Answer:

Verified
Correct Answer:
Verified
Q27: Limit pricing is a competitive strategy to
Q28: Game Types. Portray each of the following
Q29: The success of market penetration pricing strategies
Q30: Sequential games:<br>A) incorporate the possibility of an
Q31: End-of-game problem. In mid-2005, former WorldCom Inc.
Q32: Prisoner's Dilemma. In the classic characterization of
Q34: Game Types. Distinguish each of the following
Q35: When bidders on a government contract collude
Q36: Nash equilibrium:<br>A) occurs when each player pursues
Q37: Game Theory Concepts. <br>Indicate whether each of